Meteorológiai társalgó

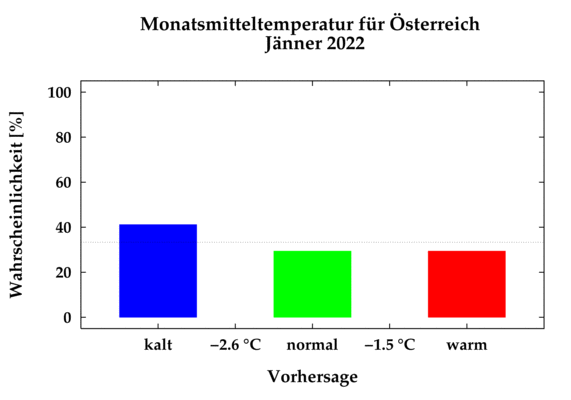
Hadd hozzak a sok matematika után egy kis nyelvtani aspektust is a háromoszlopos diagramok értelmezésének kissé hosszúra nyúlt, de számomra érdekes olvasmányt nyújtó többféle interpretációjába.

Az is okozhatja az értelmezési különbséget, hogy szó szerint, pontosabban nyelvtani értelemben, ill.a diagramot nem látva, ha valaki azt mondja:
"40% a hidegebb, 60% a nem hidegebb időszak valószínűsége"
akkor azt gondolhatnánk: 40% hideg, 60% meleg. Mert ugye: a "nem hideg" a "hideg" ellentéte (a "nem" szó), az pedig a "meleg" (és nem az "átlagos").

Ha viszont látjuk a diagramot a 3 oszloppal, a 3 kategóriával, akkor igazából csak matematikai értelemben használhatjuk, vagyis vonhatjuk össze a "nem hideg"-ben az átlagost és a melegebbet. Az egyértelműbb kijelentés ilyenkor az lenne:
"40% a valószínűsége az átlagostól hidegebb, 30% az átlagosnak megfelelő és ugyancsak 30% az átlagosnál melegebb januárnak".

És ezzel visszaérkeztünk oda, ami a ZAMG oldalán szerepel:
"Im Jänner liegt die Wahrscheinlichkeit für unterdurchschnittliche Temperaturen bei knapp über 40%. Die Wahrscheinlichkeiten für durchschnittliche und überdurchschnittliche Temperaturen halten sich mit rund 30% in etwa die Waage."

Mondtam én, hogy irigylem az osztrákokat

Nem az volt a kérdés, hogy kell-e mindenképpen az átlag megjelenítése ahhoz, hogy értelmezni lehessen egy anomália diagrammot (ez is egy vitatéma, ahol simán lehet(ett volna) egyet nem érteni kulturáltan is), hanem az, hogy miért gondolná bárki is, hogy nem lehet *erről a konkrét*, 3 oszlopú diagrammról eldönteni, hogy az átlagtól lefelé mutat több esélyt, vagy pedig fölfelé, amikor pedig de.
Ez utóbbi pedig nyilvánvaló, de azért pár módon el is lett magyarázva.

Ez megy akár napszemcsis fejek nélkül is

Biztos, hogy nem a tankönyvi Gauss volt az alap, hanem valami 30+ éves klímatikus eloszlás  De előre is köszi, ha megosztod a válaszukat. Mondjuk pár nap múlva úgy is kijön a friss futás, oszt kuka az egész

Mindenesetre emailben megkérdeztem, hogy hol húzták meg a kategória harárokat. Nem egyértelmű, s még az sem biztos, hogy becsült normál eloszlást használtak  a klímához. Szerintem elárulják, még ha nem is írták le kisbetűvel sem  

Mondom, hogy kézzel rajzoltam, így a Cpk pontossága kb kivitelezhetetlen  Csak a szemléltetést szolgálja

A Cp egészen jó de a Cpk-t még be kéne állítani.

Nyilván az osztrák kollégáknak valami hasonló valószínűségit dobott a hosszútávú, és megjelenítették a kevésbé jártasak kedvéért fehér-szüreke-fekete módon.

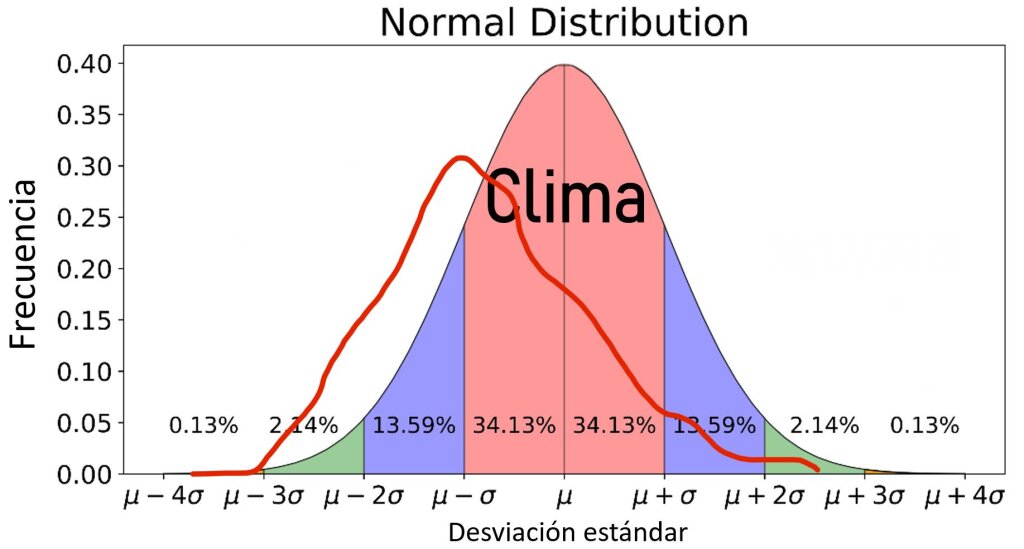
De hogy ebből a relatív függvényből miért kellett volna elhanyagolni az átlag megjelenítését azt csak az Isten + 1 tudja…
(ja és így telefonon, kézzel, móricka-ábrával nem normáltam 1-re az integrált, bocsánat )

Ami leginkább hiányzik nekem a digarammról, az a januári átlaghőmérséklet empirikus eloszlása az elmult évek (legalább 30 év) alapján. Csak ehhez összehasonlítva lehetne reálisan megítélni, hogy mit jelentenek ez egyes intervallumokba esés előrejelzett valószínűségei. Pl. nem mindegy, hogy a hideg kategóriába (-2,6°C alatti középhőmérésklet) a klima alapján 10, 20 vagy akár szélsőséges esetben 35-40% gyakorisággal esik az átlaghőmérséklet, s ehhez képest 40% körüli az előrejelzési valószínűség.

Szerk: de lehet, hogy a klimatikus eloszlás alapján meghatározott 33,3-33,3-33,3%-os gyakoriságoknak megfelelően vannak a kategoriák kialakitva, s akkor mégis tudni, hogy mihez képest kell értékelni az előrejelzett valószínűséget.

Láttatlanban is elcserélném az idei januárt a tavalyi áprilisra!
A márciusért még fizetnék is!

Az átlag az, ami a neve, ne sorold, ne add hozzá annak az esélyét, se az átlag alattihoz (hidegebb), se az átlag felettihez (melegebb).

Veled szemben nem élek vele… köszönöm.

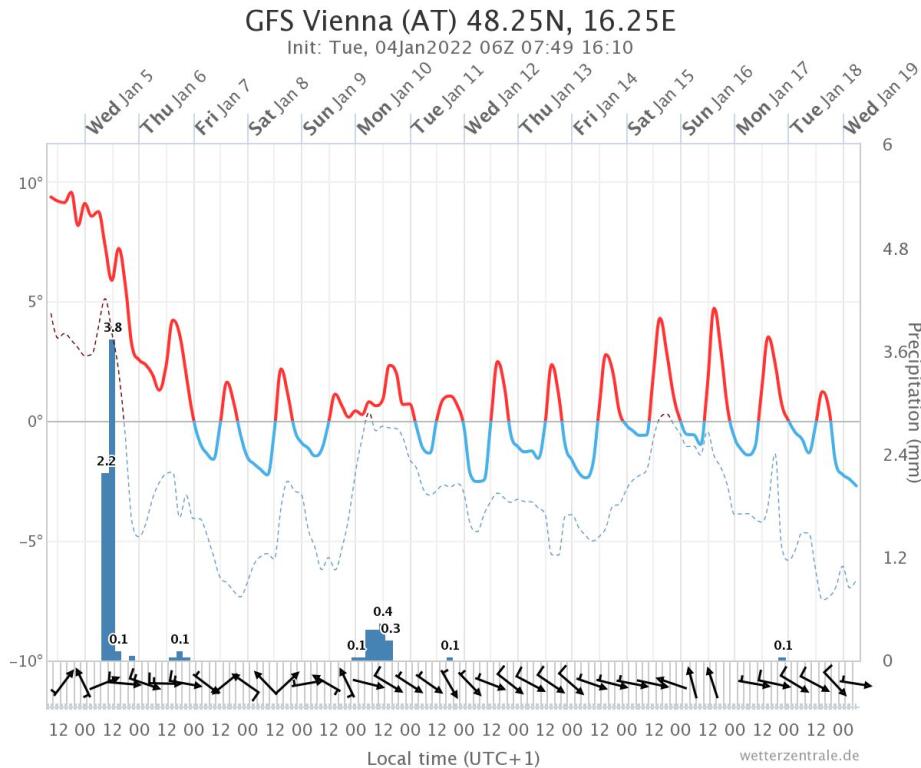
Nem úgy, mint Balassagyarmat a szélcsenddel. Még a végén akár talajmenti fagy is lehet ott január 4-én  Takt: 5,3°C

Elég jó az országos későáprilisi estéhez képest

Pedig kaptál pár esélyt..... kár.

“Donnieval soha ne állj le vitázni!”

Engedd el te is pár napszemcsissel, oszt kész

Viszont ha tovább provokálsz, tényleg kibaszlak

Ezt értem, személyes meg minden, de mi van a matekkal?
Dehogy csak nekem, látjuk, hogy mást is érdekelne

Még mindig nincs megmagyarázva az alap tévedés, mi szerint az átlagtól ne térne el a hideg felé a kérdéses ZAMG diagramm.

Ez fog menni, vagy a napszemcsik után jön a szokásos ban?
Miközben természetesen semmi valós ok nem lenne rá.

Kis segítség (lehet, tán meg se nézted, azért írsz ilyeneket)?

Neked??  Minek?!

Én tartom magam az egyik legfőbb nem-hivatalos MetNet alapelvhez; “Donnieval soha ne állj le vitázni!”

Csóri Nyuli 3 napon belül 2x baszta el  

Általában én vagyok az első, aki beismeri a tévedését, nincs abban semmi, sőt...  számtalan példa volt már rá.
Szerintem csak máshogy közelítünk a dologhoz.
Ezzel viszont nem tudok egyetérteni, de nem gond:  ""Mégegyszer: a hidegebbet keressük. Ennek a valószínűsége 40%, a nem hidegebbnek pedig 60%. És ezek alapján a hidegebb a valószínűbb?" Erre igen, a hidegebb valószínűbb a válasz."

Ráadásul már csak azért is értelmetlen az egész (szezonális előre), mert nem derül ki belőle, hogy hova szól. Egy hidegebb országos átlag nem boldogít, ha nálam közben lokális pozitív anomália van

Ugye már írod a magyarázatot?

Brutál…

Nem én jeleztem elsőnek a téves értelmezést. de komoly érdeklődéssel várom (meg szerintem még sokan itt), hogy ebből a diagrammból hogy hozod ki, hogy az átlagnál egészen picivel hidegebbnek nincs nagyobb esélye, mint akár az átlagosnak.

Eleve a normál-eloszlás félértékszélessége kell hogy legyen a referenciaérték, amihez képest szépen kiszámoljuk az 1 szigmát, 2 szigmát stb (pontosabban az mű mínusz szigmát, amit mi “hidegebb”-nek, “melegebb”-nek stb elnevezünk, de minek itt matematikázni, amikor Érden már kijött az ÚJ ÉRTELMEZÉS?    )

Volt itt kiforgatás, csak az pont a harmadik oszlop feleslegessének szólt.... A megértés szándéka nélkül.

Köszönöm, hogy objektívan leírtad elég hasonlóan.
Az igazságtalan minősítés cáfolatát pedig külön.

Szerintem ha egy színskála lenne megadva akkor kissé kékbe hajló színt kapnánk, ami átlagosnál kissé hidegebb időt jelezne.
Eléggé egyértelmű nekem mindenféle számítás nélkül.
Mondjuk Ausztriában domborzatilag is más a helyzet. Szóval ebből itt hazánkra vonatkozólag sok mindent nem szűrhetünk le.

Ahhoz, hogy az átlagosnak legyen értelme, természetesen tudni kéne emögött a módszertant. Viszont ezúttal tényleg Te tévedtél, ne vedd rossz néven, előfordul ez.
"Mégegyszer: a hidegebbet keressük. Ennek a valószínűsége 40%, a nem hidegebbnek pedig 60%. És ezek alapján a hidegebb a valószínűbb?"
Erre igen, a hidegebb valószínűbb a válasz.
(Szerk.: feltéve, hogy az "átlagos" januárok fele az átlagnál csak picit hidegebb, másik fele az átlagnál csak picit melegebb.)

* A ZAMG által (tegyük fel) futtatott 1000 modellfutásból 400 köpött hidegebb januárt, 300 amolyan átlagosat, és 300 melegebb januárt. Bárhonnan nézzük, hidegebb január a hajszállal valószínűbb a ZAMG okfejtése nyomán. 
* Ha a ZAMG nem modelleket futtatott és klaszterekbe sorolt és az alapján hozta ki ezt, hanem csak szimplán azt akarta megmondani, hogy szerinte hogy alakulhat a január, akkor tényleg hülyeség a középső (sőt, mindhárom) oszlop, adnia kellett volna egy egzakt anomália-értéket, mint az ECMWF kéthetes grafikonja számszerűen, pl. -0.6 °C vagy (normál eloszlást nézve) -0.19 °C-os anomáliát köp ki.


De erőssen túltárgyaltuk ezt a témát, viszont itt nem lettek kiforgatva a szavaid, csak tévedtél, ennyi. Felőlem repülhet a társalgóba/kukába a szál  (+remélem, a ZAMG-nak jók a számai, alpesi negatív anomália jöhetne!)

Donnie: végülis definiálva van az átlagos: a -2.6 és a -1.5 °C közötti január esélye.

Amennyiben nominális eltérést szeretnénk kimutatni, akkor olyan értelemben felesleges, hogy félre tud vezetni embereket, ahogy Téged is. 
"Ez van a grafikonon, ebből nem lehet levezetni, hogy a ZAMG januárra hidegebbet vár. Ezen mit nem értesz? "

Ezt azóta bebizonyítottuk, hogy nem igaz.
Feltételezem, hogy csak megzavart az átlagos időt jelző oszlop plusz ottléte, és nem direkt félremagyarázás volt
"Tehát szerinted az átlagos T lehetőségét nem kell felmutatni, ha az a kérdés, hogy milyen idő lesz? Erre nehéz mit mondani, önmagát minősíti."

Ki lehet mutatni külön harmadik, felesleges oszlop százalékozása nélkül is.

Ez, és a felső sor a napszemüveges vigyorgósnak is szólt.
Ha pontosan van definiálva az "átlagos" fogalma a grafikonon, akkor be lehet éppen tenni, és lehet vele is számolni, de egy nomálisan várható eltérés valószínűsítéséhez teljesen felesleges.
Mi is sokkal jobban jártunk volna, ha csak a az eltérések esélyei vannak százalékolva

A matematikai bizonyítást szókiforgatásnak beállítani: ez is önmagát minősíti, kár volt ide eljutni
Velem szemben természetesen el szabad játszani a szokásos sértődőst, ettől függetlenül érdekelne a reakciód Rudolfking vagy Tamás94 kommentjeire is.
Hogy nehogy csak sértődésnek tűnjön.

Nem akartam már reagálni, mert felesleges, de ezt nem tudom szó nélkül hagyni:

"a középső oszlop egész egyszerűen felesleges" 
Tehát szerinted az átlagos T lehetőségét nem kell felmutatni, ha az a kérdés, hogy milyen idő lesz? Erre nehéz mit mondani, önmagát minősíti.

Arra viszont megkérlek, hogy a továbbiakban ne forgasd ki a szavaimat, jó szokásodnak megfelelően, mint ahogy azt többször is tetted ma (felmutattam, hogy hol, így ne kérdezz rá).
Nem várok választ, kimagyarázkodást, semmit, mert reakciót nem kapsz rá.

Kegyetlen…

Pont az elborult (40-20-40) példát mutatja jól, hogy a középső oszlop egész egyszerűen felesleges, értelmetlen, butaság úgy, ahogy van.
Csak félrevezetésnek, téves értelmezésnek ad alapot.
Simán elég lenne 2 oszlop, 47/53% és jónapot.
Idiótaság egy átlagosnak kinevezett pontnak vagy tartománynak százalékot adni, mert úgyis ki kell venni az egyenlegből: vagy felezéssel vagy csak simán figyelmen kívül hagyással, ha nominális eltérést akarsz kapni. Vagy lehet még erőlködni pár matek függvénnyel, de teljesen mindegy, mert úgyis a két eltérésre adott százalék hozza a valódi eltérést.

Mondom, hülyék.

Tamas94: jól számoltál, köszi. Összességében a tényleg C eltérést lehet csak értelmezni, a százalékost nem annyira, mivel 0-hoz közeli negatív számokkal kell dolgozni.
Remélem most már mindenki elhiszi, amit lát

Ott van a fórumban linkelt diagrammon (#548277), hogy -2,6 és -1,5 fok közötti intervallumot tekinti "átlagosnak".
Ennél hidegebb időre 40%, ennél melegebb időre pedig 30% esély van.
Feltételezzünk normál eloszlást (jobb híján).
Ha a kalkulációm nem fals, z1 = 0,255 z2 = 0,525, így a diagramból az olvasható ki, hogy -2.05 fokos átlag helyett -2,24 fokra számítanak, ami 0,19 fokkal az átlagosnál hidegebb.
De javítsatok ki.
Javítottam a számokat, mert nem szoroztam vissza 1,1-es intervallum szorzóval.

Ez továbbra sem igaz, "nem lehet jelen grafikon alapján kimondani, hogy hidegebb lesz, de azt sem, hogy melegebb, csak azt, hogy nem lesz átlagos" - ennek a mondatnak semmi értelme a grafikon alapján. Ha se nem hidegebb, se nem melegebb időt várnának, 33-33-33%-ot kéne adniuk (vagy elborultabb esetben 40-20-40, vagy hasonló furcsaságot). Ha a hidegebb -2 fok, a melegebb +2 fok, az átlagos meg 0, akkor (40*-2+30*0+30*+2) / 3 / 100 = -0,66 °C jönne ki várható anomáliának. De mivel ez egy erősen alulspecifikált grafikon, nem tudom, mik mögötte a számok, lehet más értékekkel kéne számolni. De az biztos, hogy ezen grafikon alapján az az állítás 100%-ban igaz, hogy "a ZAMG egy lehelletnyivel átlag alatti januárra tippel".

Állítottad: nem a hidegebbnek van esélye, mert a melegebb + az átlag együtt 60%.

Tehát a "nem-hideg" esélye 60%.

A te logikád alapján a "nem-meleg" esélye pedig akkor 70%.

Akkor merre van a csúszka az átlaghoz képest?

De, pontosan ki lehet jelenteni (immár tényleg minden irányból matematikailag is bebizonyítva), hogy ezen a diagrammon összeségében az átlagtól való *enyhe* negatív eltérés, azaz az átlagnál *enyhén* hidegebb idő valószínűsíthetése látható.
Ez nem meggyőzés kérdése  hanem 100% matek.

Közben látom Rudolfking is levezette.

"Ok, hogy te 3 tényezőt veszel figyelembe, viszont hibásan értelmezed az átlag fogalmát, mert csak az egyik oldalhoz próbálod hozzátenni."
Ez sem igaz, ahogy írtam is: "Pontosan ezért azt sem lehet kijelenteni, hogy melegebb lesz, mert ahogy írtad, annak 30% az esélye, míg a nem melegebbnek 70%."
Pontosan az átlagos időjárás lehetősége (illetve a három tényező eloszlási aránya) miatt nem lehet jelen grafikon alapján kimondani, hogy hidegebb lesz, de azt sem, hogy melegebb, csak azt, hogy nem lesz átlagos.

Itt most tényleg befejeztem, nem akarok meggyőzni senkit, de nem is értek egyet a ti közelítésetekkel.

Nem velem vitázol, hanem a matematikával
Még tovább egyszerűsítem.
2 lehetőség van: 
1 - az átlag egy pont (a tényleges átlag, tized fokra).  Ebben az esetben egyből kikapható az egyenlegből, és marad az általam leírt 57 vs 43%.
(Tegyük hozzá - elég nonszensz lenne 30%-ot adni egy tizedfokos egyezésre, ezért ezt nem túl valószerű értelmezés.)
2 - az átlag egy tartomány, amely (mondjuk) egy bizonyos mértékben plusz és ugyanakkora mértékben minusz is (1-1 fokban tér el mindkét irányban).
Ebben az esetben a rá adott százalékos esély szimplán felezhető - 15-15%-ot kap mind a hidegebb, mind a melegebb verzió.
Ezzel a számítással a hideg felé eltérésnek 55, a meleg felé eltérésnek 45% esélye van.

Amint látod, a matematika elég hasonló eredményt dob ki mindkét esetben.

Ok, hogy te 3 tényezőt veszel figyelembe, viszont hibásan értelmezed az átlag fogalmát, mert csak az egyik oldalhoz próbálod hozzátenni
A diagramm összes oszlopát tekintve a legnagyobb valószínűsége 2 lehetőségből (hideg, meleg) a hidegnek van. Ebben egyetértettünk.
Amiben nem, az az, hogy a 3 oszlopot nézve is még mindig a hidegnek van a legmagasabb valószínűsége. 

Ha mindhárom oszlopot egyforma súllyal akarod nézni, akkor nem vonhatsz össze belőle kettőt tetszőlegeseb. A hidegnek az átlagos, és az enyhébb időnél is *egyaránt* magasabb az esélye. Ez van a táblázaton.

"Ha ebből a 70-ből 100%-ot csinálunk"
...hát pont ez az, ezzel pont a kiindulási alapot vágod meg. 

"Ugyanúgy hiba ha csak 60 részt (átlagos és melegebb) veszünk figyelembe, ahogy Te csináltad."
Ez nem igaz, én nem 60%-ot veszek figyelembe, hanem 60-at a 40-hez képest. 

"Ez az jelenti, hogy az átlagos hőmérséklethez képest 14%-ban a hidegebb idő felé dől a mérce."
Ez matematikailag igaz, ha 70 részt hasonlítasz össze, vagyis ha az lenne a kérdés, hogy hidegebb vagy melegebb lesz-e. A grafikon és az előre viszont azt kérdezi, hogy a január hidegebb, átlagos vagy melegebb lesz-e.

A grafikon alapján akkor lehetne egyértelműen hidegebb januárról beszélni, ha a hideg-oszlop több, mint 50%-os esélyt adna, mert akkor az átlagos vagy melegebb időnek összességében kevesebb esélye lenne.

Pontosan ezért azt sem lehet kijelenteni, hogy melegebb lesz, mert ahogy írtad, annak 30% az esélye, míg a nem melegebbnek 70%.
Az egész egy 3 tényezős dolog, Ti pedig két tényezőt vesztek figyelembe (hidegebb, melegebb).

Mindegy, nem értünk egyet, de nem gond. 

Az egész "átlagos" oszlop úgy baromság ahogy van, azaz a 3 külön oszlop marhaság. 30% esélye van, hogy PONT tizedfokra annyi lesz mint az X évi átlag? Vagy ha meg már fél fokot eltér valamilyen irányban, akkor nem egyszerűbb lenne csak a két szélső oszlopot adjusztálni? Hülyék.

Simán kellett volna egy csúszka, amin van egy átlagpont, attól elhúzni/színezni valamelyik irányban egy icipicit (alsós matek alapján), és kész.
Ez a lenti háram alapján nagyon halványan a minuszban lenne, és nem lennének félreétések, mellémagyarázások, egymás mellett elbeszélések stb.
Öreg sógor sz**kavarók lehet, direkt csinálják
Mi a "hidegebb" meg "melegebb" definíciója? 2 fok? 5 fok? Agyrém.

Igen, a (különféle) matematikai értelmezés(ek)ért köszönet nektek!

Én viszont nemcsak a meteorológia téren irigylem az osztrákokat a kiegyensúlyozottság, az adatok lehetőség szerinti "sima", kommentár nélküli bemutatása terén Az interpretációt meg bízzuk az olvasókra, nézőkre, hallgatókra...

A melegebbnek meg 30 %, a nem melegebbnek meg 70 %

Mint sok helyen, itt is az interpretáción múlik a dolog. Lásd még: félig üres, vagy félig teli a pohár?

Tán az eredeti szöveg a legkiegyensúlyozottabb, ahol ilyesféle százalékos meleg/nem meleg, ill.hideg/nem hideg "összevonás" nincs:
"... die Wahrscheinlichkeit für unterdurchschnittliche Temperaturen bei knapp über 40%. Die Wahrscheinlichkeiten für durchschnittliche und überdurchschnittliche Temperaturen halten sich mit rund 30% in etwa die Waage."

Azaz (gyorsfordítás tőlem):
".. átlag alatti hőmérsékletek kicsit 40% felett valószínűek. Az átlagos és átlag feletti hőmérsékletek 30% valószínűséggel vannak nagyjából egyensúlyban."

"De ha egy egészet 100 részre osztunk fel és abból csak 70 részt veszünk figyelembe, akkor az hiba. "

Ugyanúgy hiba ha csak 60 részt (átlagos és melegebb) veszünk figyelembe, ahogy Te csináltad.
Még mindig nem megy át, megpróbálom máshogy.

Mivel az átlagos semerre sem visz (ez lenne az esszenciája), vegyük ki.
Marad 40 hideg, és 30 meleg.
Ha ebből a 70-ből 100%-ot csinálunk, akkor a kettő aránya: 57,14% a hideg és 42,8% a meleg része.

Ez az jelenti, hogy az átlagos hőmérséklethez képest 14%-ban a hidegebb idő felé dől a mérce.
Ez nem jelentős hideget jósol, hanem egy egész picivel az átlagos alattit.

Ezekből az adatokból átlagos, vagy annál enyhébb időt kihozni a valószínűbbnek matemaikailag lehetetlen.
Az átlagos oszlopot nem csaphatod sem a hideggel, sem a meleggel szemben, se mellé. Az semmilyen matematikai számítás szerint nem működik

Konkrét celsius fokos eltérést kellene nézni egyébként is, mert a "hidegebb" meg a "melegebb" azok nem értelmezhetőek.
Ha hidegebbhez -5 fokot, az átlaghoz 0 eltérést, a meleghez meg +5 fokos eltérést társítanánk, az átlag meg lenne modjuk pont 0 fok, akkor sima szorzással kijönne, hogy -0,7 fokos eltérést várnak, ami enyhén csupán, de negatív.

Levus74: tök jó, viszont ez csak egy sima szó szerinti leírás a chartnak, de nem nevezhező értelmezésnek sem.
A matematikai Rudolfking kommentjében van, amit én is igyekezem tovább vinni.

Mégegyszer: a hidegebbet keressük. Ennek a valószínűsége 40%, a nem hidegebbnek pedig 60%. És ezek alapján a hidegebb a valószínűbb?
Épp az átlagos viszi el az egészet a nem hidegebb irányába. 
Rufolfking okfejtése akkor lenne igaz, ha csak azt vizsgálnánk, hogy hidegebb vagy melegebb lesz. De ha egy egészet 100 részre osztunk fel és abból csak 70 részt veszünk figyelembe, akkor az hiba. 

Ezt most szerintem gondold végig még egyszer.... Rudolfking már tisztán leírta matematikailag
"azaz 40%-os valószínűséggel hidegebb és 60%-os valószínűséggel nem hidegebb"

Pontosan ugyanúgy igaz, hogy  30%-os valószínűséggel melegebb és 70%-os valószínűséggel nem melegebb, az alapján ami leírtál.
Az átlag, az az átlag. Az nem visz semerre, ugyanúgy csapható mindkét eltéréshez. Nem hidegebb, és nem melegebb, tehát mindkét fenti állítás (a téid és az enyém) is igaz.

Nem, a 70%-ban ott van a 30% átlagos, ami nem hidegebb, hanem átlagos.
Az átlagos meg miért is nem számít? 

Hát, hogy teljesen őszinte legyek, tényleg hidegebb januárt vár a ZAMG, hiszen az átlagos nem számít (+- 0.5 fok mondjuk), a hidegebb és enyhébb kimenetelt összehasonlítva pedig a hideg felé billen picit a mérleg nyelve, tehát az átlagostól lehelletnyivel valószínűbbnek tartják a hidegebb kimenetelt, nyilván a hangsúly a lehelleten van 
Mert én meg így is fogalmazhatok: 30% eséllyel melegebbet vár, de 70% eséllyel átlagosat vagy hidegebbet vár a ZAMG...

Akkor mégegyszer: 40%-os valószínűséggel hidegebb, 30%-os valószínűséggel átlagos és 30%-os valószínűséggel enyhébb - azaz 40%-os valószínűséggel hidegebb és 60%-os valószínűséggel átlagos vagy enyhébb - azaz 40%-os valószínűséggel hidegebb és 60%-os valószínűséggel nem hidegebb. Ez van a grafikonon, ebből nem lehet levezetni, hogy a ZAMG januárra hidegebbet vár. Ezen mit nem értesz? 
És kérdezném a hozzászólásodat lhálykolókat is, hogy mi nem érthető...

Dehogy izgulok, van egyéb izgulnivalóm

Nem várják hidegebbre. 60%-os valószínűséggel átlagos vagy átlag feletti hőmérsékletet várnak, és csupán 40%-os valószínűséggel hidegebbet. 

Szeretnék nem hinni a 06-os GFS-nek